Volatility definition – What is volatility?
In math, volatility is a measure of how much the numbers are spread out around the mean. In Layman’s definition, volatility is how fast a certain financial asset’s price moves around its average price or mean.
What is volatility in forex trading?
Volatility measures how much the price of a currency pair fluctuates. A forex pair with a price that fluctuates wildly, hits new highs and lows, or moves erratically is considered highly volatile. For each time the price of a financial asset moves, you can imagine that the asset will also have its highest and lowest potential price to reach based on statistical values.
The industry’s common practice is that it is used as a risk indicator by analysts because they use them to determine the possibilities of the financial asset’s price to deviate from its average price. Although securities there is a lot of operating volatility, the standard deviation is the most commonly used. Suppose that we have two securities, A and B, each having a standard deviation of 2.5 and 3.0, respectively. If we compare both securities’ standard deviation, we can say that security B is riskier than A because it has a higher chance to deviate from its mean price. Therefore, the higher the volatility, the more risky trader.
How are volatility and risk related to an investment?
Volatility and risk are parts of the investment process when traders (investors) trade assets. Volatility measures how much the price of an asset fluctuates and risk is defined as the chance that a projected outcome will differ from an expected outcome. In most cases, volatility is one of the risk indicators: the higher the volatility of an instrument, the higher its riskiness. However, when volatility is too low in some cases, and the market is in a tight range, an increase in volatility can help the trader make a profit.
Conventionally financial wisdom indicates that one of the major risks of investing money is that the market is very volatile. However, some investors, especially value investors, do not believe in this conventional logic. These investors think that if the capital is permanently lost, it is the biggest risk. Both of these perspectives are not fully correct.
Investment performance is often judged, assuming that the risk involved is linked to the volatile portfolio. Some of the metrics for the measure information ratio, tracking error, in the short term and, Sharpe ratio compare the return with the portfolio’s volatility, measured concerning the benchmark or absolutely. Since the investors are usually only thinking about the returns on their investment in the short term, they will usually avoid volatility under all conditions. These conventional investors will be thrilled with a return rate below the average if there is very little volatility.
In trading, volatility risk meaning has a different explanation. When traders analyze risks, volatility risk represents the type of risks that can decrease the trader’s profitability if unexpected high volatility occurs. Mitigation of volatility risk is that traders need to decrease the trading position size or stop trading or change stop loss and targets based on the Daily Average true range (include volatility to calculate stop loss or target).
Let us see an example.
April 2018 is a good example where volatility is not a risk and an excellent opportunity. The euro weakness in April 2018 was brought about by the fact that the ECB kept the rates on hold and refused to give a timeline for the tapering and ending of the QE. So from April and several next weeks and months, volatility increased every day, EURUSD went down more and more. Bad news for EUR, increase volatility. Ity, strong bearish trend were great opportunities for traders.
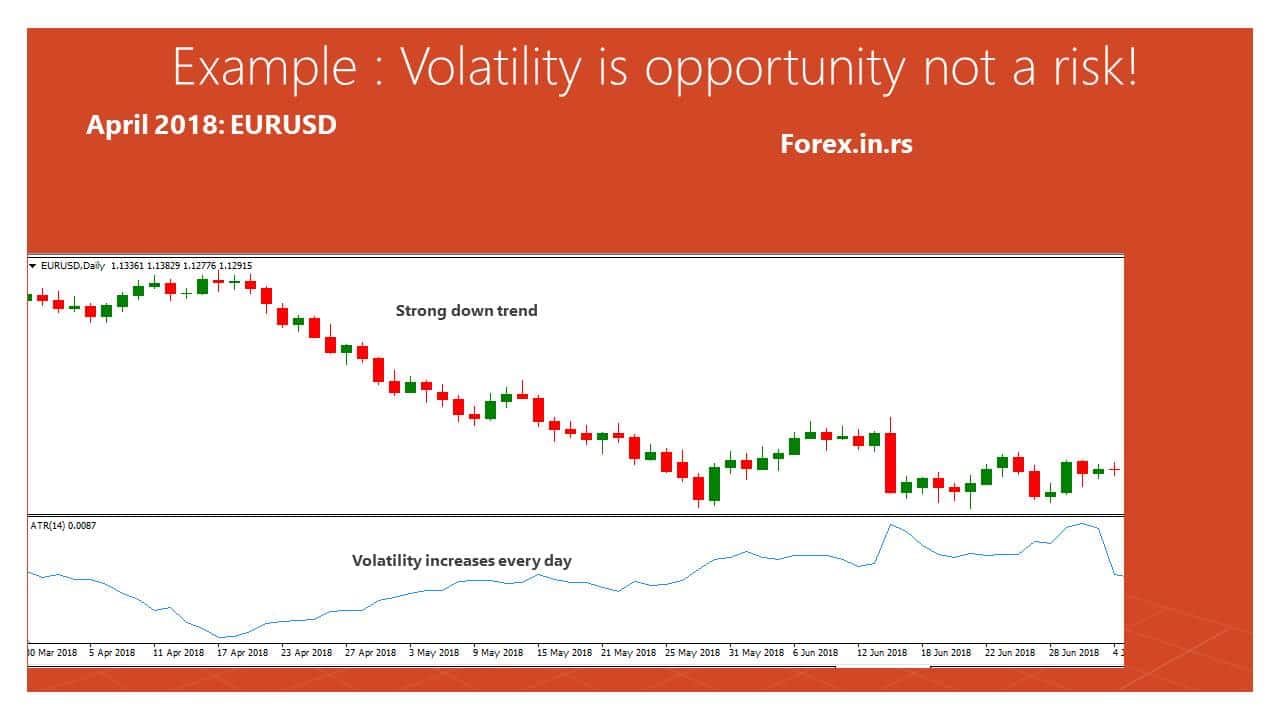
Now let us see, opposite example, in spring 20. The cause COVID 19 forex and the stock market were volatile markets. Now volatility is not an opportunity for trading, it is a more unexpected event (like an earthquake) that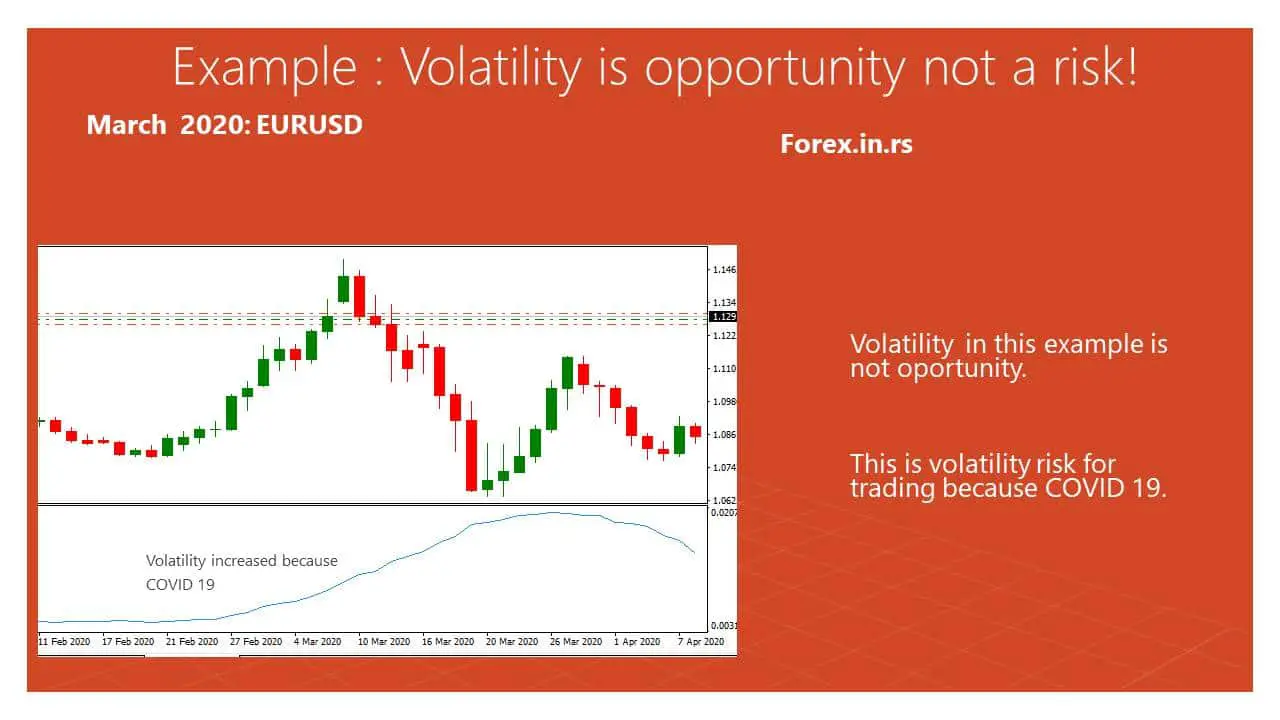
hurt the economy, and consequences can not be measured s unknown.
Risk and volatility measurement
As mentioned earlier, the common measure for volatility is the standard deviation. Other methods of determining volatility, such as computing for the asset’s beta coefficient, require more data than computing for the standard deviation.
In computing for the volatility, we will need to determine the financial asset’s mean price; it can also be called the mean return. To compute for the mean, we will have to compute for its average arithmetically or geometrically. However, in our example, we will show it arithmetically because it is more simple. In basic finance, it is also called the expected return of the asset.
The formula for computing for the mean return:
Mean = (P1 + P2 + P3 + ….. + Pn) / n
where P = price and n = number of values used.
After we compute the mean price of the asset, we can now compute its variance. Variance is the measurement of how the data is spread. It determines how far each price went when compared to its mean.
The formula for computing for the variance:
Variance = (mean – P1)2 + (mean – P2)2 + (mean – P3)2 + … + (mean – Pn)2
where Mean = average price, P = price, and n = number of values used.
The last step in computing for the standard deviation is simple; we square root the variance.
The formula for computing the standard deviation:
Standard Deviation = (variance)1/2
We can also express the exponent as 1/2; it has the same meaning as rooting the value with a square.
Therefore, the complete formula in computing for the standard deviation is:
Standard Deviation = ((mean – P1)2 + (mean – P2)2 + (mean – P3)2 + … + (mean – Pn)2)1/2
where Mean = average price, P = price, and n = number of values used.
For a practical application, assume that we will analyze stock A. It’s 5 most recent closing prices are $10, $20, $30, $40, $50, respectively.
In computing for the mean, we will have a value of $30.
Mean = (10 + 20 + 30 + 40 + 50) / 5
Mean = 30
This means that the arithmetic average of stock A’s price for the past 5 trading days is $30.
We need to compute for the variance, which is getting the deviation first then squaring it. When the mean is subtracted from its price, it is called deviation. Bestock’s stock’s low is the solution (30 – 10)2 + (30 – 20)2 + (30 – 30)2 + (30-40)2 + (30 – 50)2
Variance = (20)2 + (10)2 + (0)2 + (-10)2 + (-20)2
Variance = 1000
We can get its squared root to determine the stock’s standard deviation since we got the variance.
Standard Deviation = (1000)1/2
Standard Deviation = $31.62
The standard deviation of stock A is $31.62. This means that the price of the stock’s historical prices upwards or downwards. This helps analysts and traders in making trading decisions through risk management. Keep in mind that this measure of risk is an absolute risk of the company, and it is based on the stock’s historical prices.
Other Methods of Determining Volatility
As mention earlier, one method of computing for the volatility of an asset is computing for its beta coefficient (?). Its difference from the standard deviation is that the beta is compared with the aggregate market or index. In the United States, we use the S&P 500 as a benchmark for future returns in the equities market. Therefore, if we were to compute the stock’s beta, we will compare its performance to the S&P 500. The values of beta coefficients are usually expressed as a whole number with a decimal. For example, a beta of 1.35 means that for each 1% increase of the S&P 500 index, the stock moves 1.35 times that S&P. Therefore, we can say that a higher beta is riskier because it will be labeled as more unpredictable or its deviation from the market is huge.
Volatility is also an important variable in valuing option contracts. Since these derivatives derive their prices from a specific underlying asset, incorporating volatility is important to value the option price. Moreover, since the future is hard to predict, many analysts and traders rely on historical data to potentially have an idea of where the market might be in the future.
Volatility and value investors
Most value investors do not consider market volatility to be a risk. One of the most famous value investors, Warren Buffett, is quoted as claiming he would rather get 15% returns in the long term in lumps rather than 12% smoothly. Using this logic, many of the value investors at present are not worried about volatile markets. Their risk management strategy involves focussing on preventing capital loss permanently. These investors believe that they are emotionally strong enough to tolerate fluctuation in the short term if their strategy is proper. They get the desired result in the long term.
Investor profile linked to risk of volatility
The risk caused due to volatility is not fixed; it depends to a large extent on the profile of the investor. Some of the different investor profiles and the effect of volatility on the investment results are discussed.
Long-term investors with high-risk tolerance: These investors are looking at returns over a longer time period, like ten years, since they wish to save money for their retirement or college expenses for children. Due to their behavior, these investors are not affected by volatility. These will persevere with their investment plan, though the market is volatile. These investors do not consider volatility as a risk. They are more concerned about the annual returns on their investment in the l term and ensure that there no loss to their capital permanently during this period.
Short term investors will typical short-term results of their investment port monitored years of investing. For these investors, the market volatility low prices the capital at the end of the period will be affected by the short-term results. These investors closely monitor the volatility since it will force them to sell their investment at low prices, resulting in losses.
Long term investors with low-risk tolerance. Due to their personal behavior, these investors are affected by market volatility. Though these investors have long term goals, they may take investment decisions against these goals because of market news, volatility in prices, or other short term conditions. These investors do not behave rationally when they hear negative news, and so they sell at lower prices, though this is not required. This investor category should consider the risk due to volatility since having a more volatile investment will result in low financial returns.
Long term investors who spend a small amount of their portfolio consistently: These investors include individuals who use a small part of their investment portfolio for their expenses every year or endowments, charities, which spend 5% of the investment portfolio to cover their operational expenses annually. Though volatility matters to some extent, it is not the main risk involved.
Historical Volatility and Implied Volatility for determining option prices
Historical volatility takes the data of the underlying asset historically. This type of volatility affects the historical performance underlying asset and measures the fluctuations in the data series. In practice, historical volatility is not used in forecasting the prices of options contracts because it reflects the analyst’s expectation. This can provide traders valuable insight into how the underlying security is performing presently compared to the past.
On the other hand, implied volatility incorporates the analyst’s expectations to determine the potential price of the future’s underlying asset. However, it cannot also be regarded as a “forecast” because volatility looks at the probability of how much will price deviate from its average. But in the case of implied volatility, it is looking forward to the future and does not incorporate historical values in computing it.
Conclusion
Hence, while choosing the investment, it is important to understand the client profile to determine the most suitable portfolio volatility. It is always better to advise the client to invest in longer terms and tolerate fluctuations in the portfolio’s value. This will help the investment manager maximize the long-term returns without bothering about volatility so that the client will have a major advantage over other investors.
Volatility is not a risk, but sometimes it can be, and then we talk about risk volatility. It doesn’t look effortless, but it is not. Let we see what Warren Buffett said about volatility and risk:
“Volatility is not a measure of risk. And the problem is that the people who have written and taught about volatility do not know how to measure — or, I mean, taught about risk — do not know how to measure risk. And the nice about the beta, which is a measure of volatility, is that it’s nice and mathematical and wrong in terms of measuring risk. It’s a measure of volatility, but past volatility does not determine the risk of investing.”
Warren Buffett
He is an expert in financial niche, long-term trading, and weekly technical levels.
The primary field of Igor's research is the application of machine learning in algorithmic trading.
Education: Computer Engineering and Ph.D. in machine learning.
Igor regularly publishes trading-related videos on the Fxigor Youtube channel.
To contact Igor write on:
igor@forex.in.rs
