Understanding the way growing annuities work could help you in better managing your savings. The formulas and the calculations required for every investment could be baffling. Still, once you understand the math behind them, it becomes a lot simpler to recognize what your annuity calculator is doing behind the scenes. To know more about growing annuities and break it down into simple terms, let us first look at what a growing annuity is, followed by its future value and its connection with the present value.
A growing annuity is nothing but a stream of equal cash flows that grow at a constant rate, but what is the future value of a growing annuity?
The future value of the growing annuity represents the total amount of money after a series of payments that are growing (or declining) at a constant rate during a certain time period. Usually, each payment is increasing at a specified growth rate (i.e. each payment is 7% larger than the last payment).
The future value of a growing annuity formula can be calculated by working out each individual cash flow by growing the initial cash flow, finding the future value of each cash flow at the interest rate, and then summing up all the component future values.
PV of growing annuity formula is:
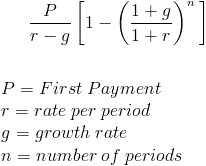
Ordinary annuity vs. growing annuity
Please do not confuse it with the ordinary annuity. The ordinary annuity also involves periodic cash flows, but these remain constant, while in a growing annuity, these cash flows keep growing. There are several examples of a growing annuity. A common example is a rental contract. If you have ever rented out a property as an owner, you might have noticed a clause in the contract that ensures an increase in the annual rent amount at a constant rate. Another great example of a growing annuity is a company’s dividend. If the company follows a growth model encompassing several stages, there might be at least one stage in the model where, in a certain period, the dividends will grow at a fixed rate.
Last week we wrote an article about the Present Value of Growing Annuity. Let us see how the Future Value of a growing annuity example.
Future value of growing annuity – with example
The formula could easily obtain the future value of a growing annuity.
FV = P [{(1+r)^n – (1+g)^n}/(r-g)],
FV is the future value of the growing annuity, P is the first payment to the annuity, the rate per period is r, g is the growth rate, and the total number of periods is denoted by n.
Let us understand this formula by taking a look at an example. Let us say you wish to put off a portion of your paycheck every year in the amount of $4000 for the first year. The amount you save in the annuity every year varies because your pay rises by 8% every year. If your annuity account’s rate is 2% per year, how much would you save at the end of 5 years? Let us substitute the formula with all the values we know.
Here, P = $4000, r = 0.02, g = 0.08, and n = 5.
Hence, the calculation looks like this: FV = 4000[{(1+0.02)^5 – (1+0.08)^5}/(0.02-0.08)]. When evaluated, this comes to $24,349.86. This means, at the end of 5 years, your growing annuity account would have about a total sum of $24000.
Link to the present value of growing annuity
If you already know your growing annuity’s present value, it becomes simpler to calculate the future value. The present value is concerned; it could be multiplied by (1+r)^n to get the future value. To understand this better, let us take a look at the formula of present value. PV = {P/(r-g)} * [1-{(1+g)/(1+r)}^n]. PV here is the present value, and all the other variables are the same as in the formula of the future value. So, assuming you have the present value in front of you, it is a piece of cake to estimate the future value.
Takeaway
Once you understand the logic behind the formulas that estimate your savings, it is easy to identify which investment modes would return the maximum value for your hard-earned money. The formulas behind the calculations should hopefully help you make much more informed decisions.